machining Archives - Hill Engineering

Case Study: Multi-step machining distortion modeling

by Robert Pires

Distortion of parts during the machining process is a significant problem faced by many machining vendors. This phenomenon typically results from the release and redistribution of residual stress in the material once the part is unclamped from the machine table. When not accounted for, machining distortion can lead to out-of-tolerance parts that either require reworking, or have to be scrapped. Continue reading Case Study: Multi-step machining distortion modeling

Machining distortion modeling with multi-step models including residual stress

Distortion of finished parts during machining is a significant problem which typically results from release and redistribution of residual stress in the material once the part is unclamped from the machine table. If not accounted for, can lead to parts out of tolerance that need rework or become scrap. Hill Engineering’s machining process simulation capability solves the problem of reducing uncertainty in machining planning and improving machining processes by providing results from validated models to support decisions for contract machining vendors who want to produce high-quality parts efficiently and OEMs who want to maximize the productivity of their supply chain.

This case study focuses on machining modeling of a representative aircraft specimen using multi-step finite element analysis. Machining modeling was used to identify a machining strategy that requires less machine time (e.g., fewer part set-ups) to arrive at the final geometry, while also reducing the distortion of the finished part. The results illustrate how multi-step machining models can be used to provide upfront estimates of distortion, as well as guidance to optimize machining processes and obtain improved machining outcomes.

The part geometry considered in this case study is shown in Figure 1, and was designed to be representative of an aircraft part. The overall dimensions are 25 x 10 x 2.5 inches. The pockets, stiffener walls, holes, and tapering along the 25 inch dimension and 2.5 inch dimension provide a complex and representative geometry. The part is assumed to be machined from a 27 x 12 x 3.5 inch plate of aluminum alloy 7050-T7451 (stress relieved by stretching). While this material state typically exhibits low levels of residual stress, distortion during machining can still occur depending on the part geometry, machining strategy, and required tolerances.

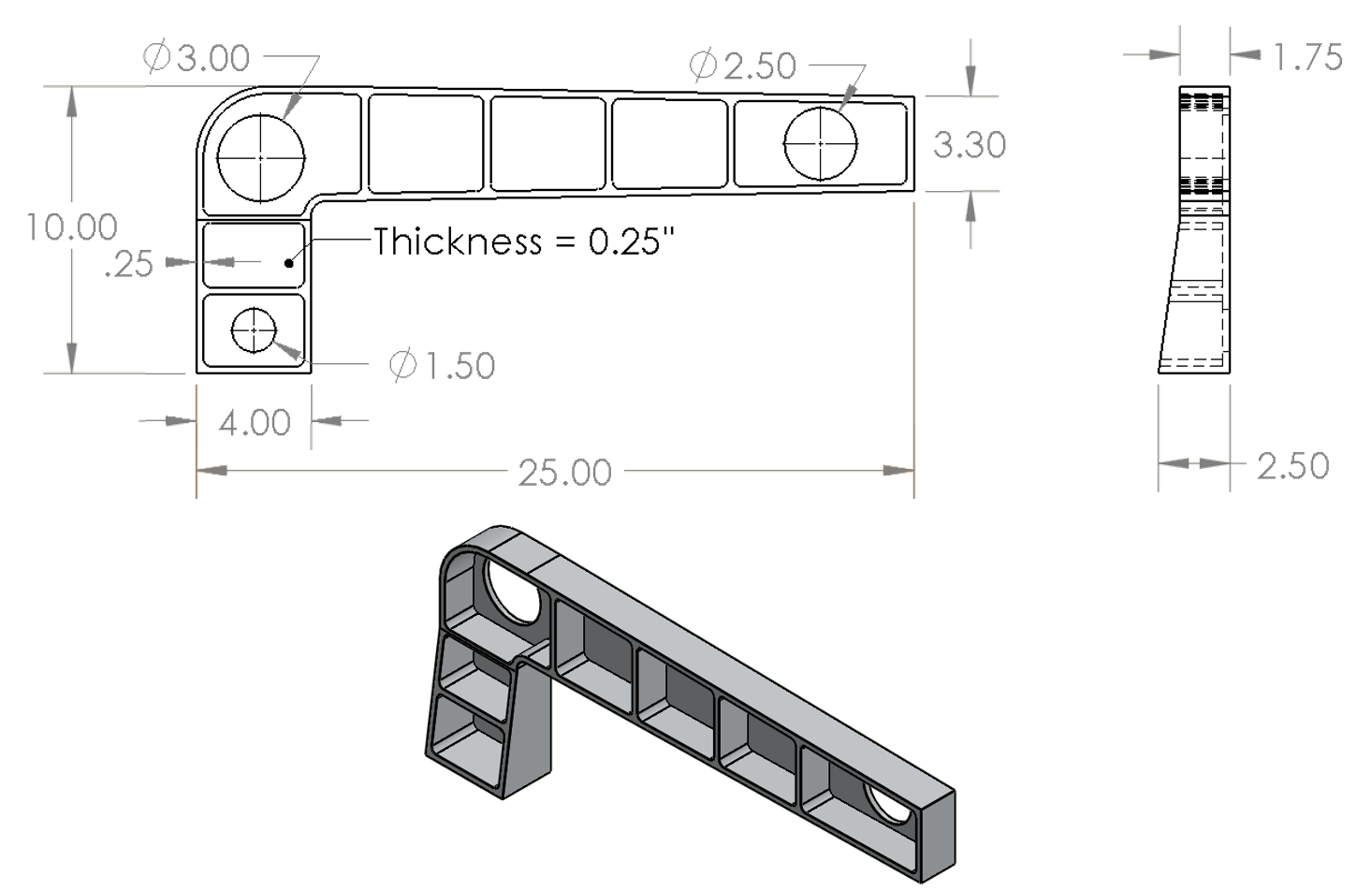
Part geometry (dimensions in inches)

The plate considered for machining this part provides extra material coverage on all sides. Figure 2 shows the amount of machining cover on each side, given the part is aligned with the mid-thickness of the stock plate with equal spacing relative to the sides of the stock. One inch of extra material is available on all sides when looking from a top view, while one-half inch of extra material is available along the thickness direction.

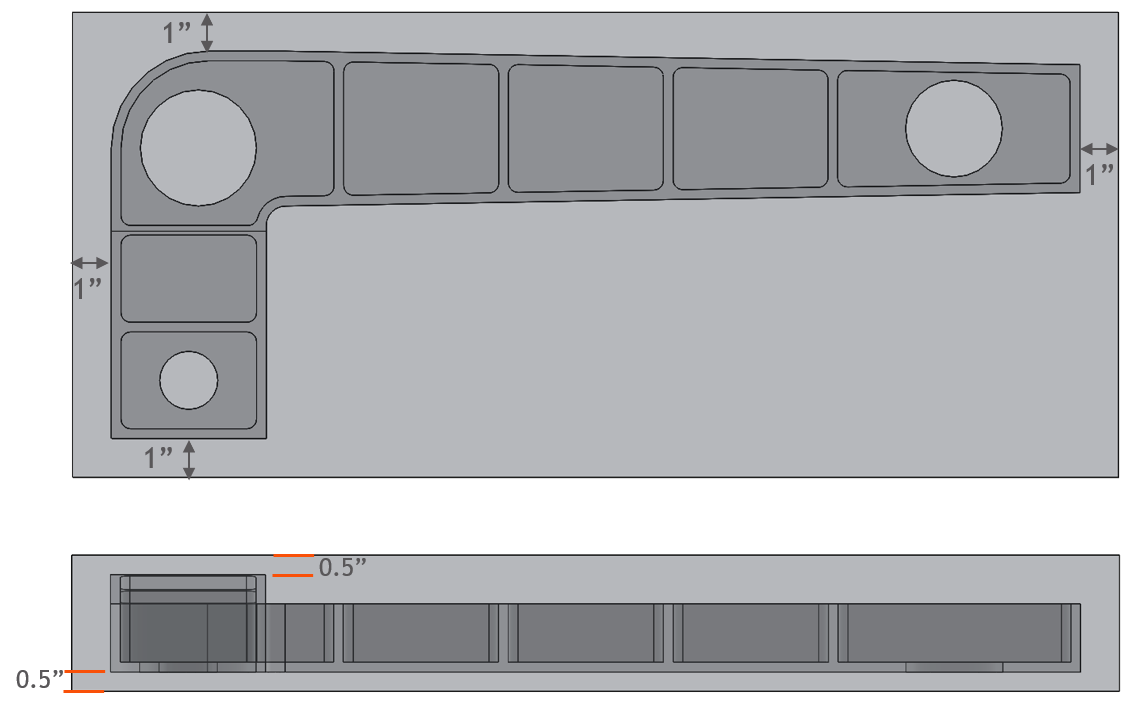
Part geometry within stock material when placed at the mid-thickness of the plate

The assumed residual stress in the stock plate material is shown in Figure 3. This is based on slitting method results published in [1] for 3-inch-thick plate of aluminum alloy 7050-T7451. The residual stress distributions are relatively symmetric and were normalized and scaled for the specific stock plate thickness used in the current study (3.5 inches). The rolling direction of the stock plate was assumed to be along the 27-inch dimension of the plate.

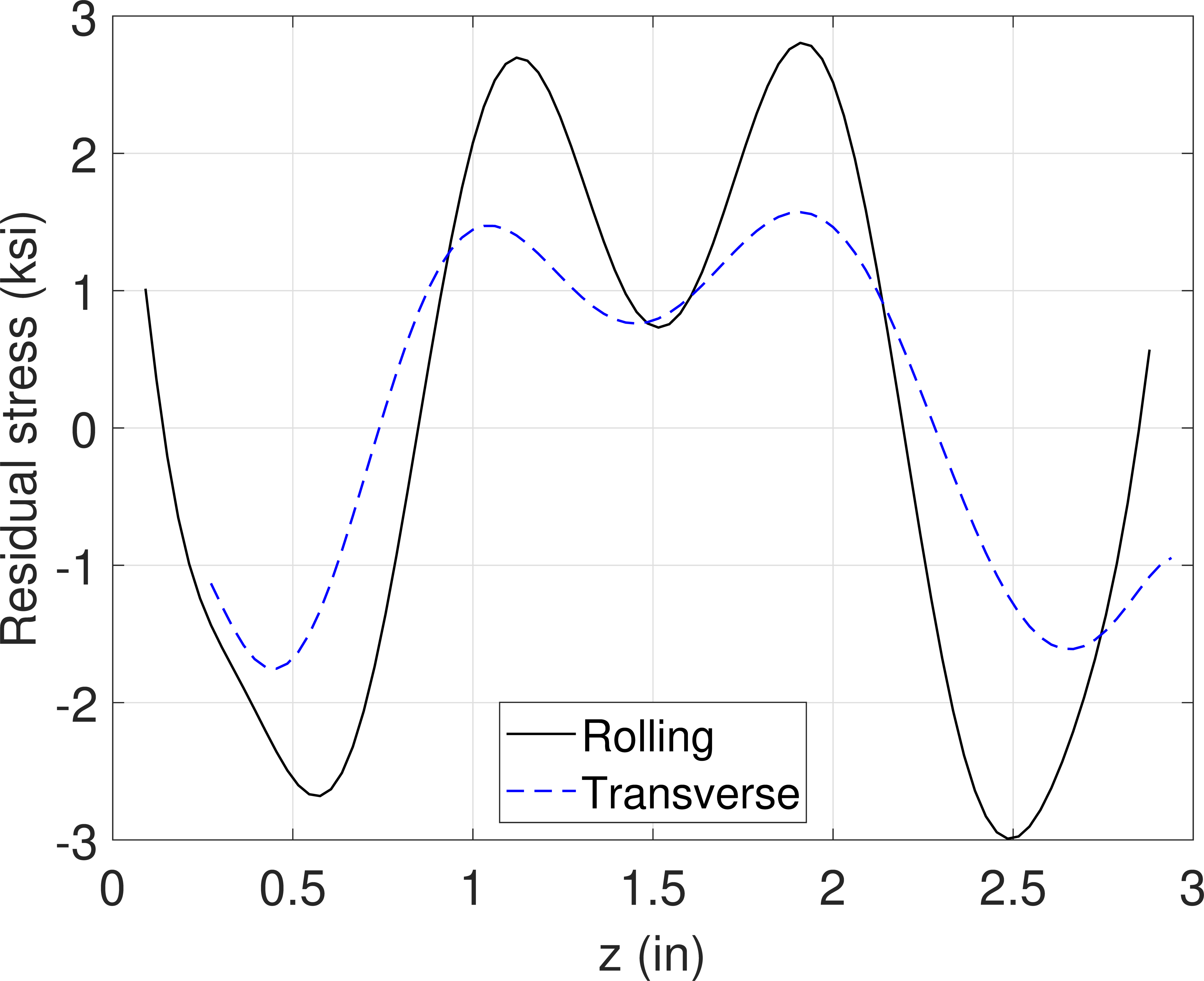
Residual stress measured in aluminum alloy 7050-T7451 plate (adapted from [1])

The baseline machining strategy considered is illustrated in Figure 4, in which the part is placed near the top surface of plate. Step 1 includes a rough machining pass on the bottom surface of the plate to obtain a flat surface for subsequent machining. Then, the part is flipped on the machine table. Step 2 involves an initial rough machining of the pockets and stiffener walls. Step 3 flips the part once again and finalizes machining of the bottom flat surface of the part. Finally, the part is flipped for the last time, and machining of the pockets, holes, and stiffener walls is finalized to arrive at the final geometry. This machining strategy includes a total of 3 flips on the machine table.

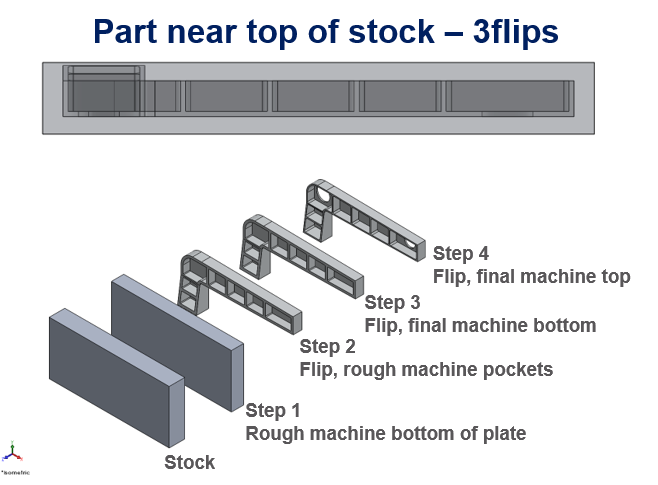
Part placement and baseline machining strategy

Multi-step finite element models were employed to obtain estimates of the distortion and residual stress at the end of each machining step. For brevity, the displacement of the finished part only (step 4) is shown here. Figure 5 shows a contour plot of the displacement along the z-axis (U3, perpendicular to the bottom flat surface of the part) on a scale that varies from -0.025 to 0.025 inches. The displacement U3 range (maximum minus minimum value) is about 0.030 inches. Maximum displacement is observed near the corner region of the part that contains the 3-inch diameter hole (shown in Figure 1).

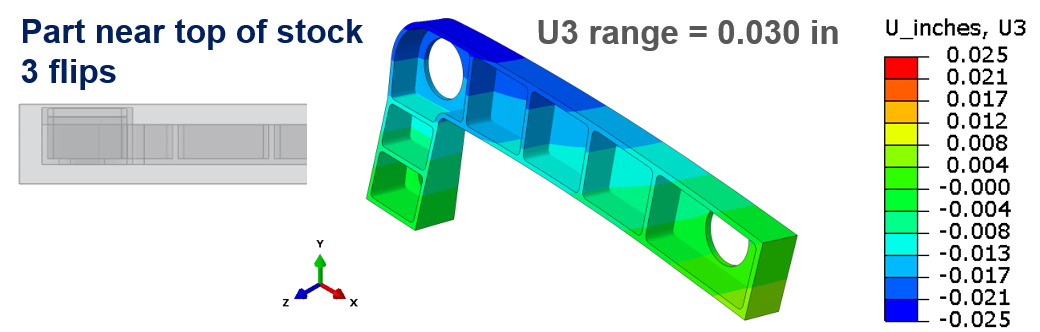
Contour plot of displacement along the z-axis (U3) for the finished part from the baseline strategy

Modeling was performed to simulate many different machining approaches. The optimal machining strategy places the part at the bottom surface of the stock plate as illustrated in Figure 6. The first step involves rough machining of the pockets and stiffener walls. The part is then flipped, and final-machined on the bottom flat surface. The second and final flip on the machine table provides the setup to final-machine the pockets, holes, and stiffener walls. This machining strategy uses a total of 2 flips (one less than the previous strategy).

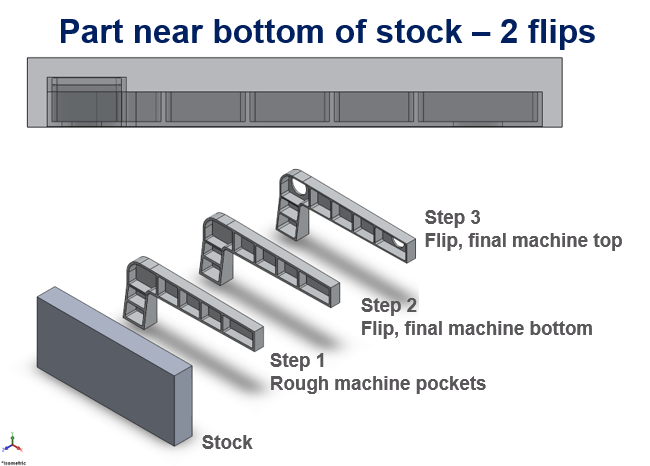
Part placement and optimized machining strategy

The part distortion for the optimized machining strategy is shown in Figure 7 (using the same color scale as in Figure 5). Compared to the baseline strategy (Figure 5), a different displacement pattern is observed, although the maximum values are near the same region (i.e., near the corner of the part with the 3-inch diameter hole). The displacement range is 0.013 inches for the optimized machining strategy, which is significantly lower than observed from the baseline approach (0.030 inches). It is important to note that the optimized strategy (which places the part near the bottom of the stock) not only provided a finished part with lower amount of distortion, it also required less machine time (fewer flips), which represents an improvement in efficiency of the machining process.

Contour plot of displacement along the z-axis for the finished part from the optimized strategy

This case study considered multi-step machining models of a representative aircraft specimen, including the residual stress in the incoming stock material, to assess the distortion of the finished part. Two different machining strategies were presented, which included differences in part placement within the stock material, and sequence of machining steps. The results identify an optimized machining strategy that uses fewer flips on the machine table (setups) to arrive at the final geometry, while also reducing the distortion of the finished part. The results illustrate how multi-step machining models can be used to provide upfront estimates of distortion and guidance to optimize machining processes in order to obtain improved outcomes. Please contact us for additional information.

Machining distortion modeling

Part distortion during machining is a significant problem in many industries, particularly where rigorous dimensional tolerances are required. Distortion of finished parts can lead to significant economic loss and should be managed for effective design and production. This case study demonstrates some of the basic concepts related to the impact of residual stress on part distortion during machining. A representative problem is defined, and a model is used to estimate part distortion due to machining of raw material containing bulk residual stress.

This study considers a 304.8 x 203.2 x 12.7 mm (12.0 x 8.0 x 0.5 inch) aluminum plate as the starting raw material for the analysis. From the plate an example part will be machined that has the same in-plane dimensions as the starting plate (304.8 mm x 203.2 mm) and includes a 2.54 mm (0.1 inch) thick frame around a 2.54 mm (0.1 inch) thick web.

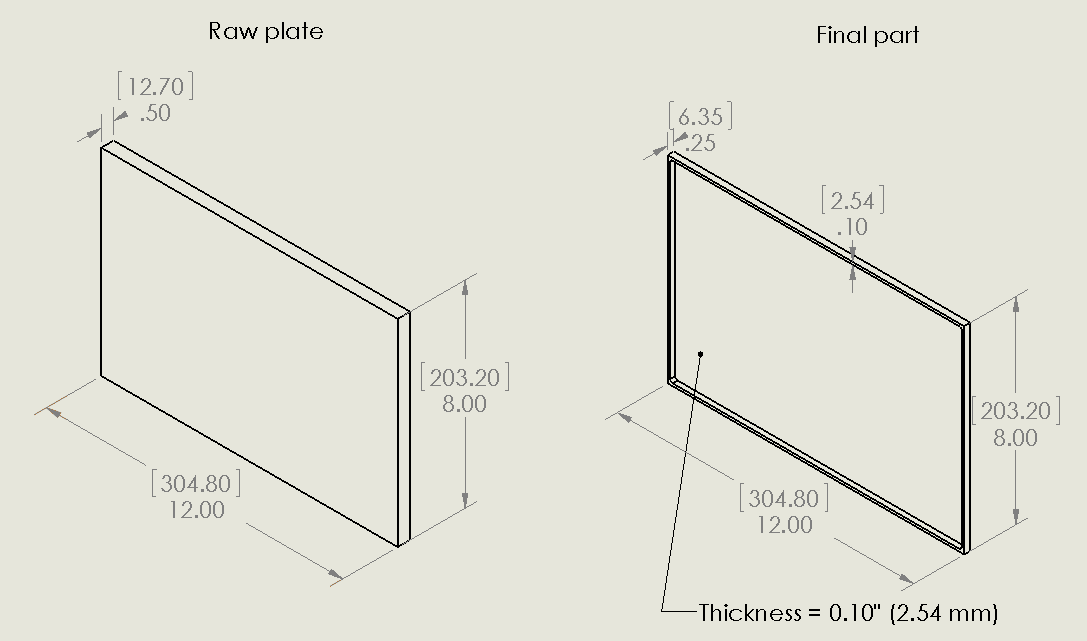
Raw plate and final part geometry. Non-bracketed dimensions are in inches and bracketed dimensions are in mm.

Aluminum plate is often stress relieved by stretching, and typically exhibits low levels of residual stress post-stress relief. For the sake of this analysis, the raw material is assumed to have the residual stress distribution shown in Figure 2a (similar to the residual stress measured by Prime and Hill [1]). The residual stress values are low compared to the yield strength of the material, ranging from about -20 to 20 MPa (-3 to 3 ksi).

In addition to the bulk residual stress present in the raw material, the machining process also induces stress. The machining-induced residual stress assumed for this demonstration is shown in Figure 2b, and exhibits a typical distribution with compressive residual stress near the machined surface that spans over a thin layer (0.2 mm) before it reaches magnitudes near zero. The peak compressive residual stress at the machined surface is -50 MPa (~ 7.3 ksi). The bulk residual stress in Figure 2a is assumed to be present in the raw plate for the analysis, while the machining-induced residual stress in Figure 2b is applied locally to the machined surfaces.

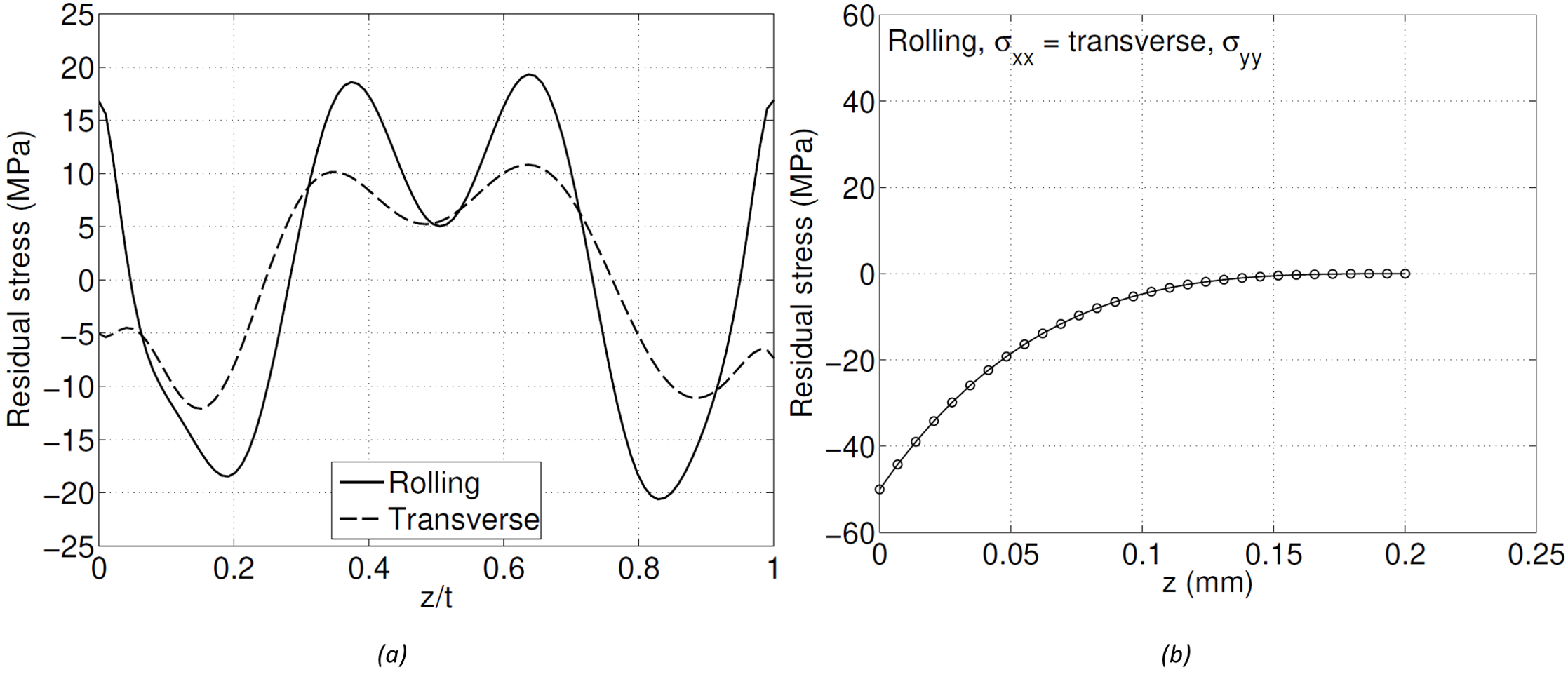
(a) Bulk residual stress (similar to [1] along rolling and transverse direction, (b) idealized machining induced residual stress

A finite element model including the bulk and machining-induced residual stresses was used to predict the distortion of the finished part. The model is elastic and superposes bulk and machining residual stress to provide an equilibrium solution. Figure 3a shows the deformed shape (using a magnification factor of 30 to better illustrate the deformation). The displacement pattern shows bowing of the finished part with respect to its intended shape, with positive displacements near the center. A 2D map of the displacement of the bottom surface of the finished part is shown in Figure 3b. Line plots along the x direction at y = 101.6 mm and along the y direction at x = 152.4 mm are shown in Figure 3c. The distortion range is approximately 1.4 mm. It is important to note that even though the bulk residual stress in the raw material is low (about 5% of the yield strength), it still has potential to cause significant distortion in finished parts, as illustrated here.

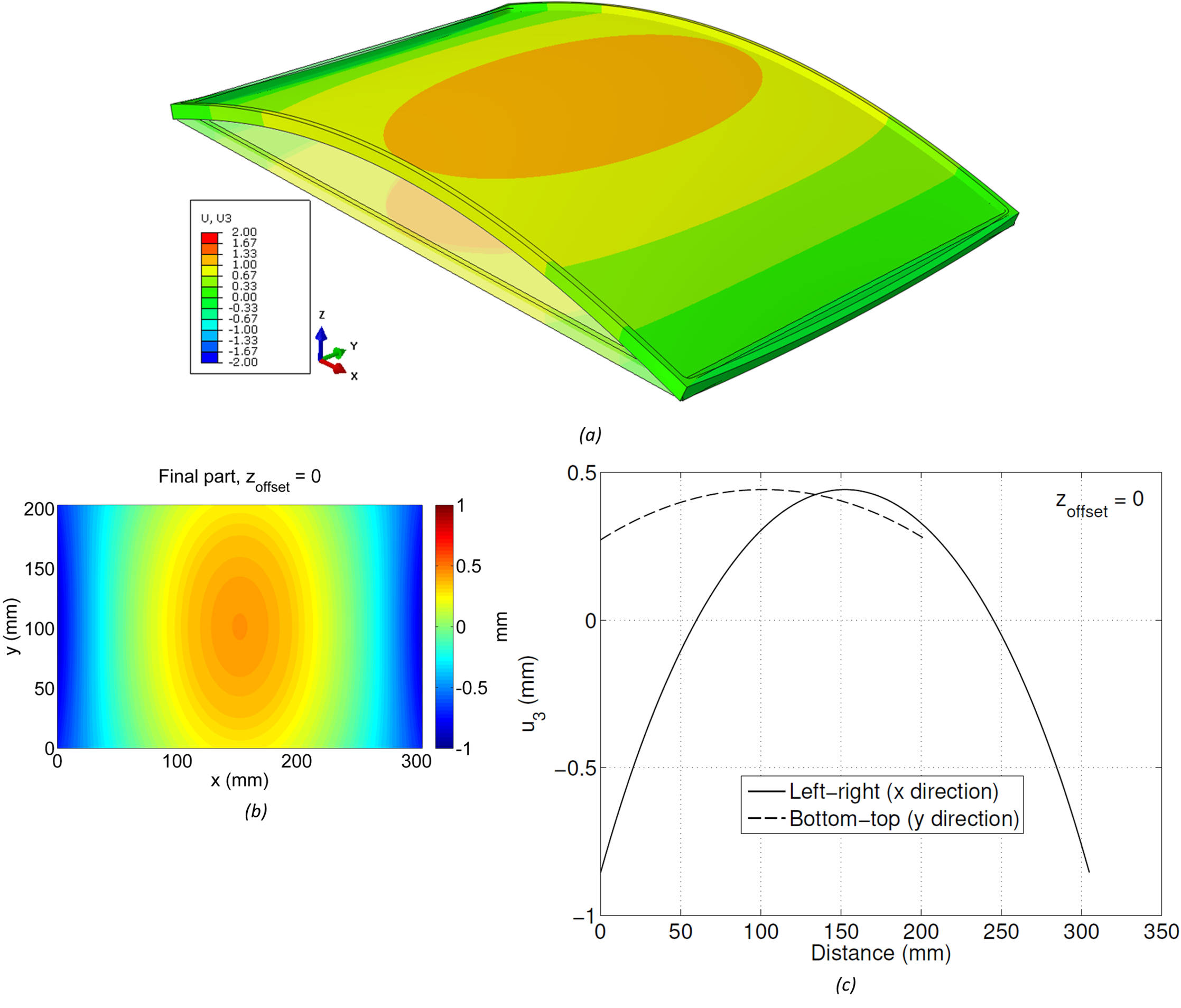
(a) Undeformed/deformed 3D shape of final part with zoffset = 0, (b) 2D map of leveled displacement of bottom surface, (c) line plots along paths from left-right and bottom-top

Since the raw plate is thicker than the final part, the final part can be extracted from different positions through the thickness of the raw plate (e.g., Figure 4). The position from within the raw plate that the final part is removed from can have a significant impact on the distortion (due to the different bulk residual stress levels at different locations through the thickness). The position is defined by an offset distance from the bottom surface of the raw plate, zoffset. In the first example, the zoffset = 0, i.e., the bottom surface of the final part is aligned with the bottom surface of the raw plate (z = 0).

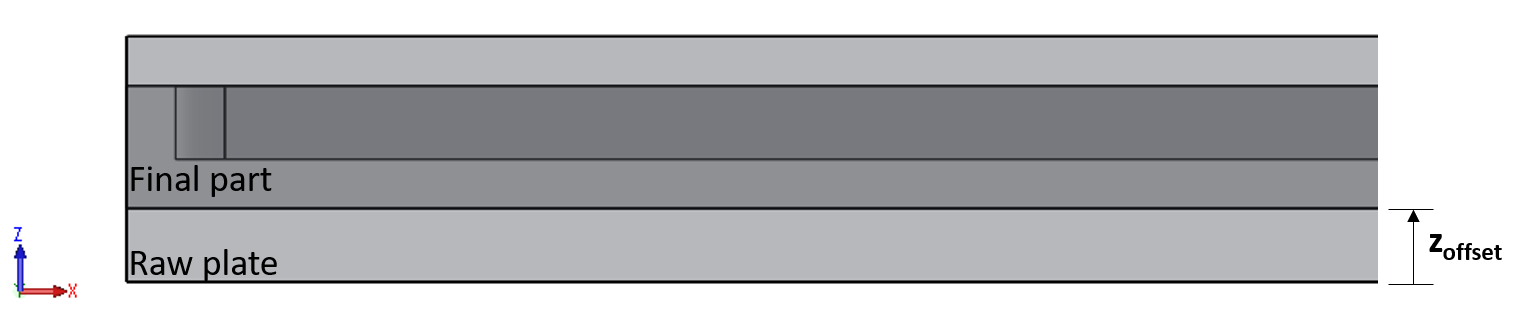
Location of machining of baseline/final part within the raw plate

The model used here can be modified to consider different part placements within the raw material in a straightforward manner. A significantly different result was obtained considering zoffset = 2.54 mm (0.1inch), which is shown in Figure 5. An opposite pattern of distortion is observed in Figure 5a compared to the case where zoffset = 0 (Figure 3a). The 2D map shown in Figure 5b shows displacements that range from 1.1 mm to -0.6 mm. Figure 5c shows the displacement along the left-right and bottom-top paths, and includes the results obtained with zoffset = 0 for comparison. Compared to zoffset = 0, zoffset = 2.54 mm exhibits displacement along the x direction that ranges from positive-negative-positive values and with higher magnitudes. The displacement along the y direction is similar for both offsets, but have opposite signs.

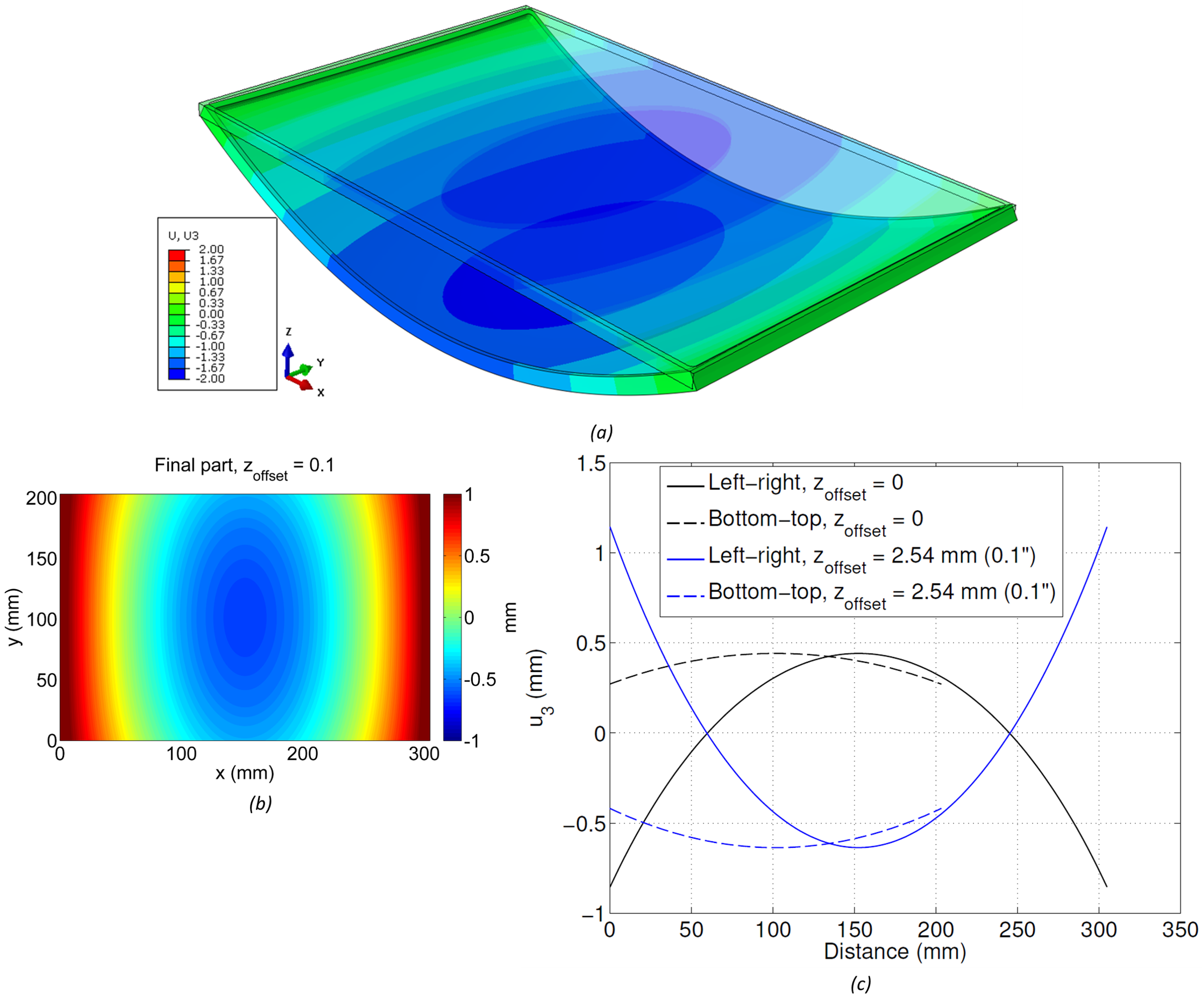
(a) Undeformed/deformed 3D shape of final part with zoffset = 2.54 mm (0.1inch), (b) 2D map of leveled displacement of bottom surface, (c) line plots along paths from left-right and bottom-top comparing zoffset = 0 and 2.54 mm

Another aspect that influences the part distortion is the thickness of the web of the large pocket. The previous results considered a thickness of 2.54 mm (0.1inch), as illustrated in the final part drawing in Figure 1. Reducing the thickness to 0.635 mm (0.025inch) and considering the zoffset = 0 configuration causes significant changes in the results, as observed in Figure 6. A similar pattern of distortion is observed in Figure 6a and Figure 6b compared to Figure 3a and Figure 3b, however the magnitudes of displacement are significantly lower. A line plot comparing the results obtained with both thicknesses is shown in Figure 6c. Overall, the model with reduced thickness (red lines) provides lower displacement magnitudes along both paths (left-right and bottom-top) compared to the initial model with 2.54 mm thickness, and exhibits peak displacement that is lower by about 50%.

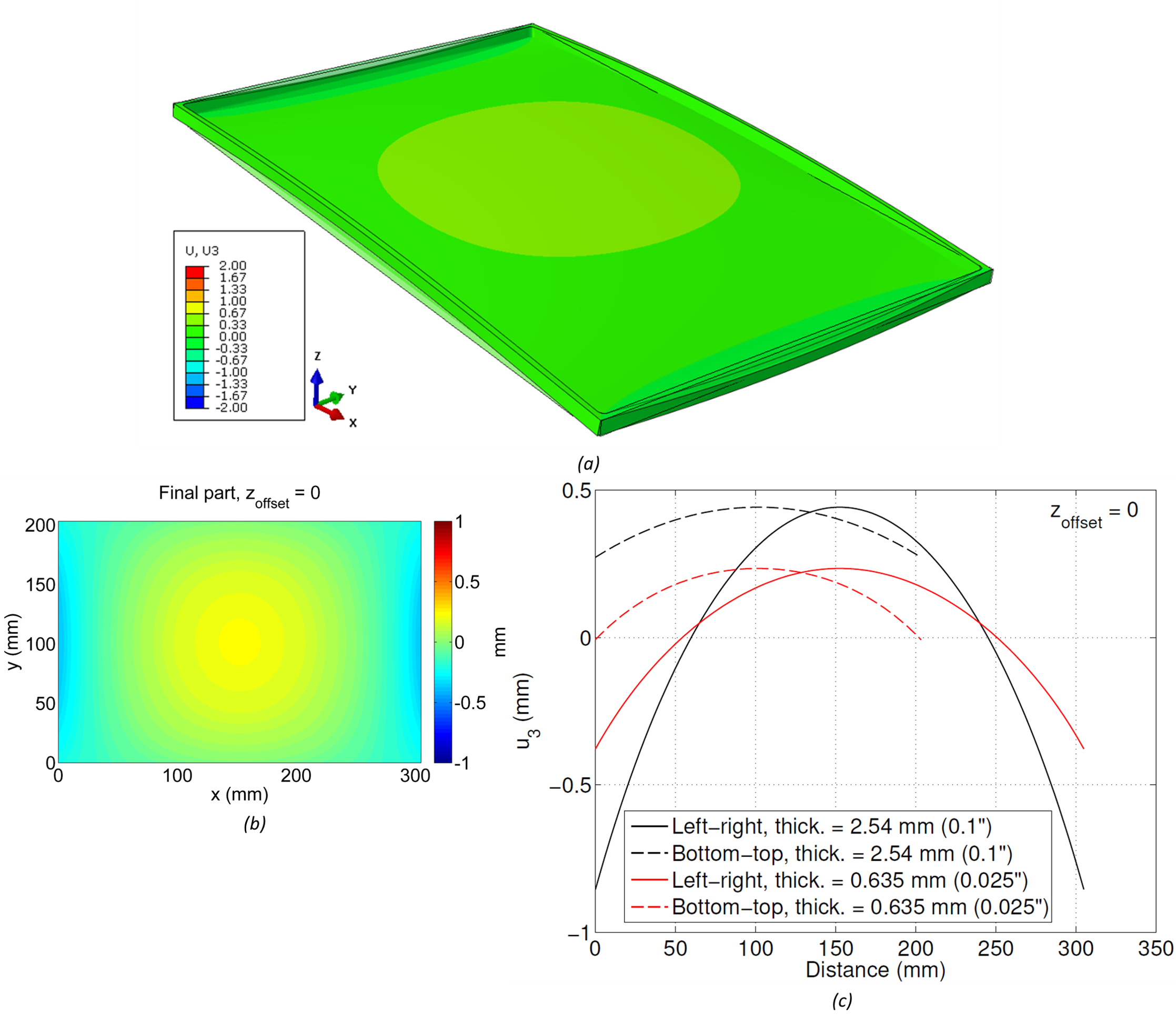
(a) Undeformed/deformed 3D shape of final part with zoffset = 0, (b) 2D map of leveled displacement of bottom surface, (c) line plots along paths from left-right and bottom-top comparing thickness = 0.635 mm (0.025inch) and 2.54 mm (0.1inch)

This case study provided an example problem for the estimation of part distortion due to residual stress release from machining, considering a typical bulk residual stress distribution and machining-induced residual stress distribution. The results show significant part distortion, even though the considered bulk residual stress had very low magnitude compared to the yield strength of the material. The results also show that part distortion varies significantly depending on the machining location within the raw stock material.

For more information concerning this case study or any of the residual stress measurement techniques employed at Hill Engineering, feel free to contact us.

[1] M. B. Prime and M. R. Hill, “Residual stress, stress relief, and inhomogeneity in aluminum plate,” Scripta Materialia, pp. 77-82, 2002.